순열 사이클 분할의 성질
읽는 사람이 순열 사이클 분할(이하 순싸분)이 뭔지에 대해서는 안다는 가정 하에 글을 작성한다.
'순열 사이클 분할'이라는 키워드로 검색하면 순싸분이 무엇인지 쉽게 알 수 있을 것이다.
Codeforces에 순싸분이 자주 나오는 것 같다.
예전부터 순싸분이 나오면 탈탈 털렸었다...
근데 뭐 순싸분 자체가 어려운 개념은 아니니까... 가만히 있었는데 며칠 전에 또 털렸다.
https://codeforces.com/contest/1768/problem/D 이 문제인데, 본 대회에서 80분동안 못풀었다....
본 대회때 고민 + 오늘 다시 업솔빙하다가 알게 된 성질에 대해 한 번 정리를 해보려고 한다.
이를 대충 아시는 분들은 글을 읽을 필요없이 맨 아래의 결론과 생각이 일치했는지만 비교해보면 좋을 것 같다. 혹시 다르다면 댓글을 남겨주시길...
이번에 알게된 성질은 cycle의 개수, 순열에서의 SWAP연산, 순열에서의 Inversion의 개수와 관련이 있다. 관련 문제가 codeforces, atcoder, BOJ (특히 유사코)에 꽤 많이 있는 것 같다.
이 글에서 말하는 cycle의 개수는 순열 사이클의 개수를 의미한다.
또, 이 글에서 말하는 SWAP 연산은 순열의 두 원소를 교환하는 것을 의미한다.
아래와 같은 예시를 보자. 2번 인덱스와 5번 인덱스의 값을 SWAP하였다.
| 인덱스 | 1 | 2 | 3 | 4 | 5 | 6 |
| 값 | 4 | 2 | 5 | 3 | 6 | 1 |
| 인덱스 | 1 | 2 | 3 | 4 | 5 | 6 |
| 값 | 4 | 6 | 5 | 3 | 2 | 1 |
마지막으로, 이 글에서 말하는 Inversion의 개수란 다음과 같다.

이제 본격적으로 내가 찾은 몇 가지 성질들을 살펴보자..
1. SWAP 연산을 한 번 진행하면 Inversion 개수의 parity가 달라진다.
이 말이 뭐냐면... 일단 예시를 살펴보자. 1 4 2 3이라는 순열에 1번의 SWAP 연산을 적용한 결과들을 정리해 보았다.

기존 Inversion의 개수는 2개(짝수) 였지만, 1번의 SWAP 연산 후에는 모두 홀수개가 된 것을 확인할 수 있다.
이 예시뿐만아니라 어떠한 예시를 살펴보아도 그렇다. 이제 증명을 해보자.
값이 각각 x와 y인 두 수를 SWAP한다고 해보자. 순열이기 때문에 x와 y는 서로 다른 값이다.
증명은 x < y이면서 x가 y보다 앞에 있는 경우만 할 것이다. 이를 증명하면 나머지 세 경우는 같은 방식으로 매우 쉽게 증명할 수 있을 것이다.
SWAP 전의 모습을 그림으로 나타내면 아래와 같다.

이때, 각 영역에는 원소가 없을 수도 있다.
암튼 이 상황에서 x와 y를 SWAP해보자.

A 영역에서 x와 inversion 관계였던 원소들은 SWAP 후에도 x와 inversion 관계일 것이다.
또, A 영역에서 x와 inversion 관계가 아니었던 원소들은 SWAP 후에도 x와 inversion 관계가 아닐 것이다.
x와 A영역 간의 위치 관계가 변하지 않았기 때문이다.
마찬가지로 y와 C 영역의 관계도 마찬가지다.
즉, 두 원소를 SWAP하여도 그 원소들 바깥 쪽에 있는 원소들(A, C영역)과는 inversion 관계가 바뀌지 않는다.
그렇지만, B영역의 원소는 다르다. inversion의 개수가 어떻게 변할까?
B영역에서 값이 x보다 작은 원소의 개수를 p개,
B영역에서 값이 x보다 크고 y보다 작은 원소의 개수를 q개,
B영역에서 값이 y보다 큰 원소의 개수를 r개라 하자.
그렇다면, x와 y를 SWAP하면, inversion의 개수는 다음과 같이 변한다.
(inversion의 개수) = (SWAP 전 inversion의 개수) + ( -p + q + r ) + ( p + q - r ) + 1 = (SWAP 전 inversion의 개수) + 2q + 1
여기서 ( -p + q + r )은 x와 B 영역 원소들간의 inversion 개수 변화량이고,
( p + q - r)은 y와 B 영역 원소들간의 inversion 개수 변화량이고,
1은 x와 y간의 위치가 바뀜으로 생기는 inversion이다.
홀수개만큼 변한다는 것을 증명하였다.
아마 여기까지 이해했다면 x < y이면서 x가 y보다 앞에 있는 경우뿐만 아니라 나머지 경우에 대해서도 그렇다는 것을 쉽게 알 수 있을 것이다.
2. SWAP 연산을 한 번 진행하면 싸이클의 개수가 1 증가하거나 1 감소한다.
참고로 위 사실때문에 SWAP 연산을 한 번 진행하면 싸이클 개수의 parity가 변한다는 것도 쉽게 알 수 있다. (1 증가하거나 1 감소하기 때문이다.)
랜덤하게 1 증가하거나 1 감소하는 것은 아니고, SWAP하는 두 원소가 같은 싸이클에 있었는지에 따라 달라진다.
이를 먼저 정리하면 아래와 같다.
(i) SWAP 하려는 두 원소가 같은 싸이클에 있는 경우
-> SWAP 후, 싸이클의 개수가 하나 증가한다. (두 원소가 속해있던 싸이클이 두 개로 나눠지기 때문이다.)
(ii) SWAP 하려는 두 원소가 서로 다른 싸이클에 있는 경우
-> SWAP 후, 싸이클의 개수가 하나 감소한다. (두 원소가 각각 속해있던 두 싸이클이 하나로 합쳐지기 때문이다.)
왜일까?
두 경우 모두 그림을 그리면 쉽게 알 수 있다. 아래 두 예시를 보자.
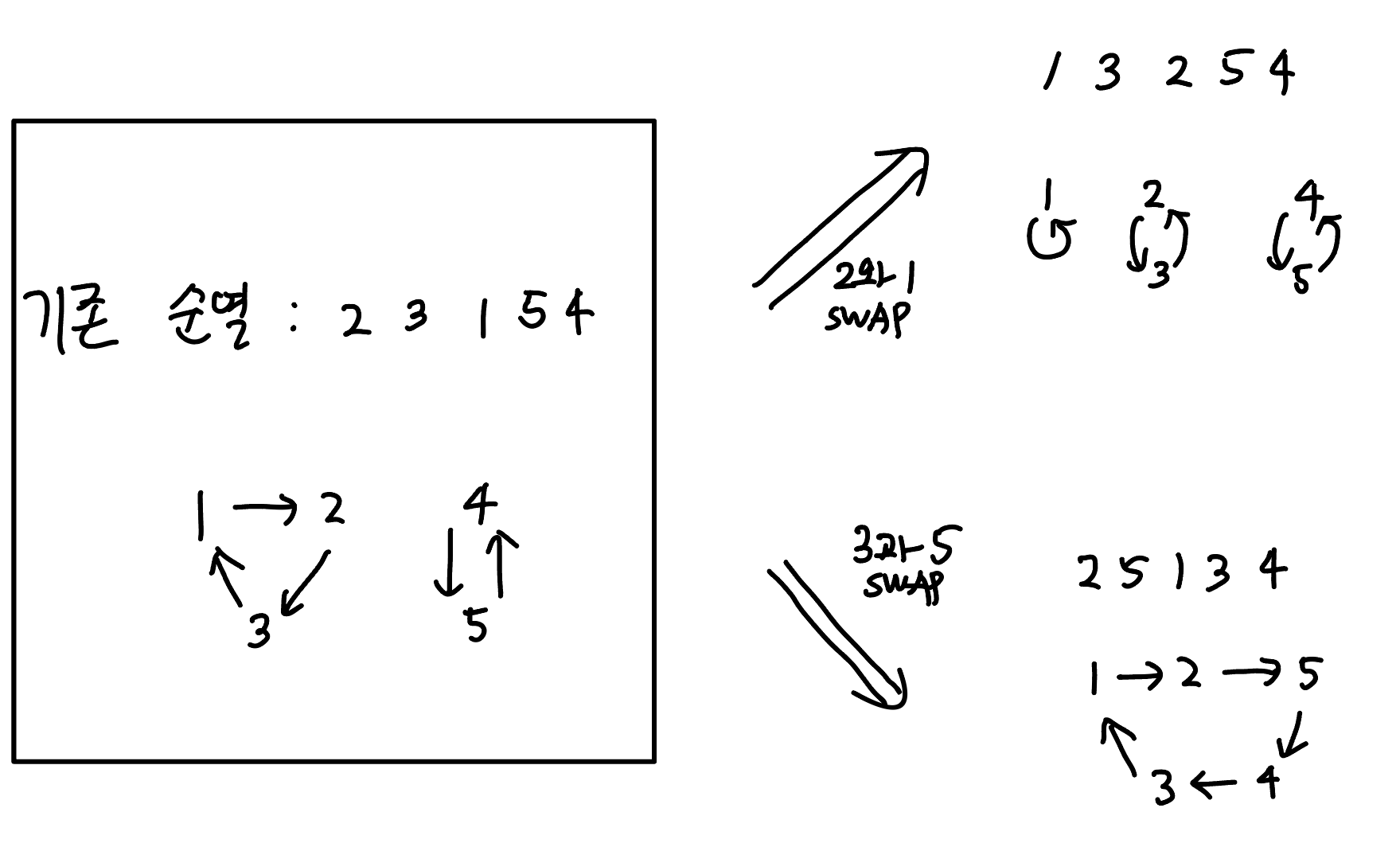
2와 1은 SWAP한 것은 같은 싸이클에 있는 원소를 SWAP한 경우이고, 3과 5를 SWAP한 것은 서로 다른 싸이클에 있는 원소를 SWAP한 경우이다.
위와 같은 예시를 몇 개 직접 해보면 왜 싸이클이 나눠지고 합쳐지는지 쉽게 알 수 있을 것이다. (ㄹㅇ이다. 귀찮아서 그런 것이 아니다.)
(간선을 삭제하고 추가한다는 느낌으로 생각해보자.)
결론
1. SWAP 연산을 한 번 진행하면 Inversion 개수의 parity가 달라진다.
2. SWAP 연산을 한 번 진행하면 싸이클의 개수가 1 증가하거나 1 감소한다.
이를 정리해보자.
SWAP 연산
Inversion의 parity 변화
싸이클 개수가 1만큼 변화
싸이클 개수의 parity 변화
네 가지가 모두 연결되어 있다고 보면 된다!
신기하다....
암튼 이러한 성질들을 자기들끼리만 알고 쉽게 쉽게 문제를 풀고 있었던 것 같다! ㅡㅡ
나는 라이브 때 이러한 성질들을 어느정도 발견했었는데, 이것을 진작 알고 있었으면 문제를 해결할 수 있었을 것 같다. 이를 증명하느라 많은 시간을 쓰게 되어 문제를 풀지 못했었다....
또 위 성질들에 의해서 다음과 같은 사실을 쉽게 알 수 있다.
서로 다른 N개의 원소를 정렬을 하기 위해 필요한 최소 SWAP 횟수는 (N - 싸이클 개수)와 같다.
관련 문제
문제를 먼저 읽어보거나 풀어본 뒤, 보면 좋을 것 같다.
아래에 있는 두 문제 외에도 관련 문제를 몇 개 추천받았는데, 풀어본 뒤 하나씩 추가할 예정이다.
boj.kr/25577 열 정렬정렬 정
사실 이 글을 쓰게 된 이유이기도 하다. 위에서 말한 코포 D를 틀리고 추천 받은 문제였다. 나는 그냥 그리디(?)하게 앞에서부터 SWAP하면서 쉽게 해결하였다. 싱글벙글 S1 혹은 G5를 기여하려고 기여창에 갔는데 뭔가 심상치 않았다. 태그도 순싸분이 붙어있고, 웰노운이라고 하더라... 이땐 뭐가 웰노운이라는지 몰랐는데, 아마 내가 쓴 이 글의 내용을 말하는 것 같다. (아님 말고..)
좌표압축을 통해 순열로 만들어 풀면 된다.
단순히 앞에서부터 올바른 값을 찾아 SWAP하는 방식으로 해결할 수 있다. 그리디하게 이득이기 때문이다. 이 풀이도 마냥 쉽지는 않은 것 같다.
소스: http://boj.kr/771468bdf9f749c194d48b6b4cdddf68
그치만 우리는 이제 조금 더 간단한 풀이를 생각해볼 수 있다. ㅎㅎ
우리는 순열 싸이클의 개수가 N개가 되게 만들고 싶다.
SWAP 연산 한 번 당 싸이클의 개수는 1 변화한다. 모든 싸이클을 두 개의 싸이클로 나누는 작업을 반복하여 N개의 싸이클로 만들면 된다. 한 번 나눌 때마다 한 번의 연산이 필요하다.
즉, 답은 (N- 처음 싸이클의 개수)이다.
https://codeforces.com/contest/1768/problem/D
이제 이 문제를 쉽게(?) 풀 수 있다. 문제에 대한 기본적인 이해를 했다고 가정하겠다.
문제에선 Inversion의 개수가 1이 되는 상태를 원한다고 하였다.
즉, 아래와 같은 상태를 원한다.

우리는 위와 같은 상태 중 하나를 만들어야 하고, 그 중 최소 SWAP 횟수를 구해야 한다.
위 사진에서 빨간색으로 표시된 이웃한 두 원소를 k와 k+1이라 하자.
이제, 위의 n-1가지 경우를 만들기 위한 SWAP횟수 중 가장 작은 값을 구해야 한다.
주어진 순열에서 k와 k+1이 같은 싸이클에 있다면 그 두 개는 나누지 않고 나머지 모든 원소를 나누는 횟수와 같다.
서로 다른 싸이클에 있다면 N개의 싸이클로 나눈 후, 두 원소를 합치는 한 번의 SWAP을 더 하면 된다.
이를 이용하면 쉽게 답을 구할 수 있다. 위에서 설명한 boj.kr/25577 처럼 N개의 싸이클을 만드는 데 필요한 SWAP횟수는 (N - 처음 싸이클의 개수)이다. 이를 ans라 하자.
(i) k와 k+1이 같은 싸이클에 있는 경우: 답이 ans - 1 이다.
(ii) k와 k+1이 다른 싸이클에 있는 경우: 답이 ans + 1 이다.