[백준] 열혈강호 시리즈 (C++)
최근에 신촌 연합 중급반에서 flow에 대해 배웠다.
나에게는 어려워서 거의 이해하지 못한 상태로 수업이 끝났다.
최근 며칠 동안 영상도 다시 보고, 종만북을 한 번 읽었더니 좀 감이 잡힌 것 같다.
그래서 야심한 새벽에 강의 연습문제에 있는 열혈강호 시리즈를 풀어보았다.
플래티넘 막 푸니까 정말 재미있는 듯? ㄹㅇㅋㅋ
열혈강호 문제가 1~6까지 있더라.
1. boj.kr/11375
2. boj.kr/11376
3. boj.kr/11377
4. boj.kr/11378
5. boj.kr/11408
6. boj.kr/11409
일단 방금 1, 2, 3을 풀었기 때문에 간단하게 풀이(그래프 모델링방법?)를 남겨보려고 한다.
조만간 시간이 나면 열혈강호 4, 5, 6도 풀어보아야겠다. (업뎃 예정) (2/8 열혈강호4 추가완료)
그림이 발퀄이니 조심하자.
1. 열혈강호 (11375)
회사에 직원이 N명, 일이 M개있다.
근데 각 직원은 한 개의 일만 할 수 있고, 각각의 일을 담당하는 사람은 1명이어야 한다.
다음과 같이 모델링하면 된다.
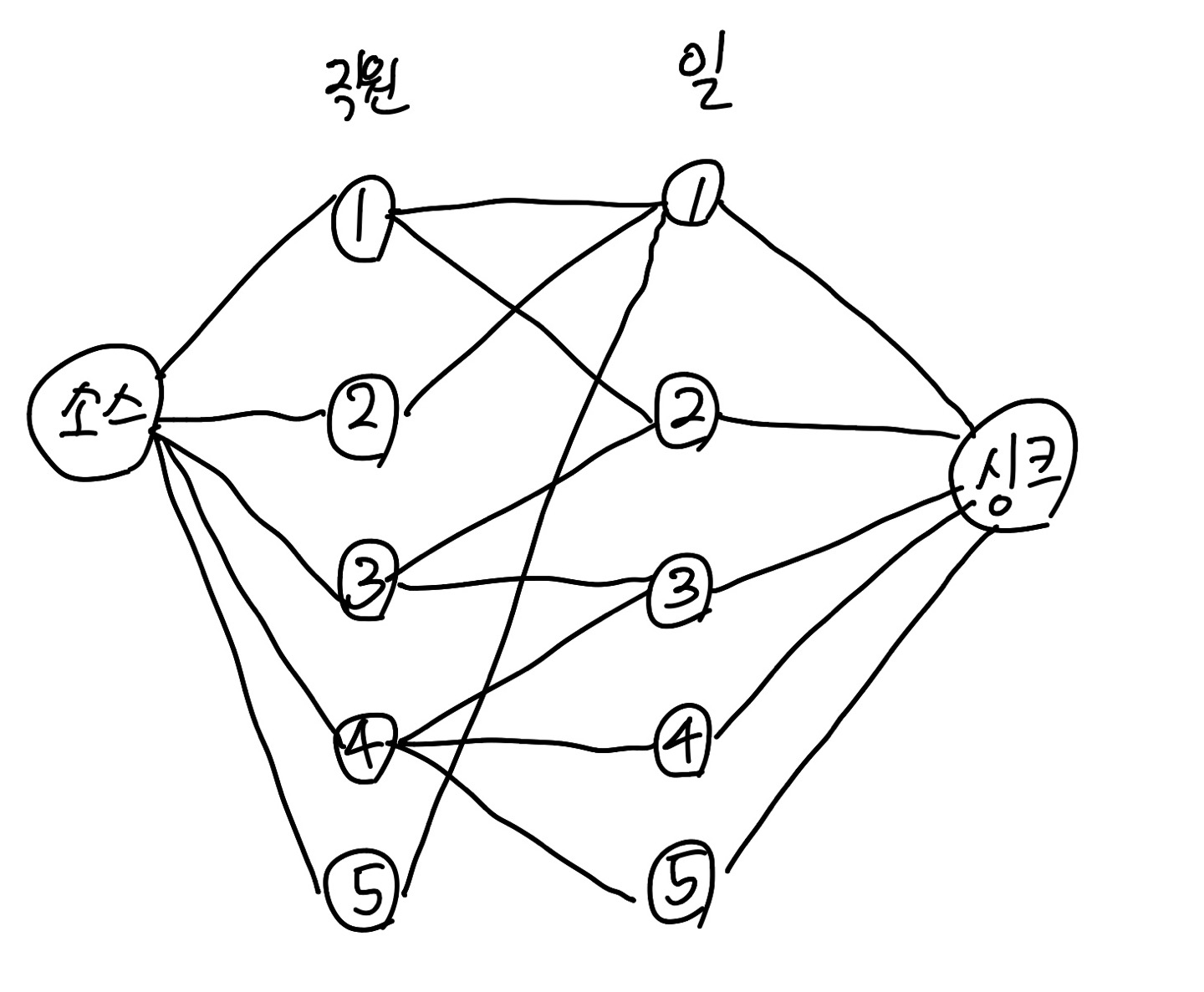
왜 가중치가 다 1이냐면
소스->직원의 가중치 : 직원마다 할 수 있는 일이 한 개라고 했으니까
직원->일의 가중치 : 1보다 크기만 하면 상관없다.
일->싱크의 가중치 : 각 일마다 담당하는 사람이 1명이니까
2. 열혈강호2 (11376)
이 문제는 열혈강호(11375)와 다 같지만, 각 직원은 최대 2개의 일을 할 수 있다.
다음과 같이 모델링하면 된다.
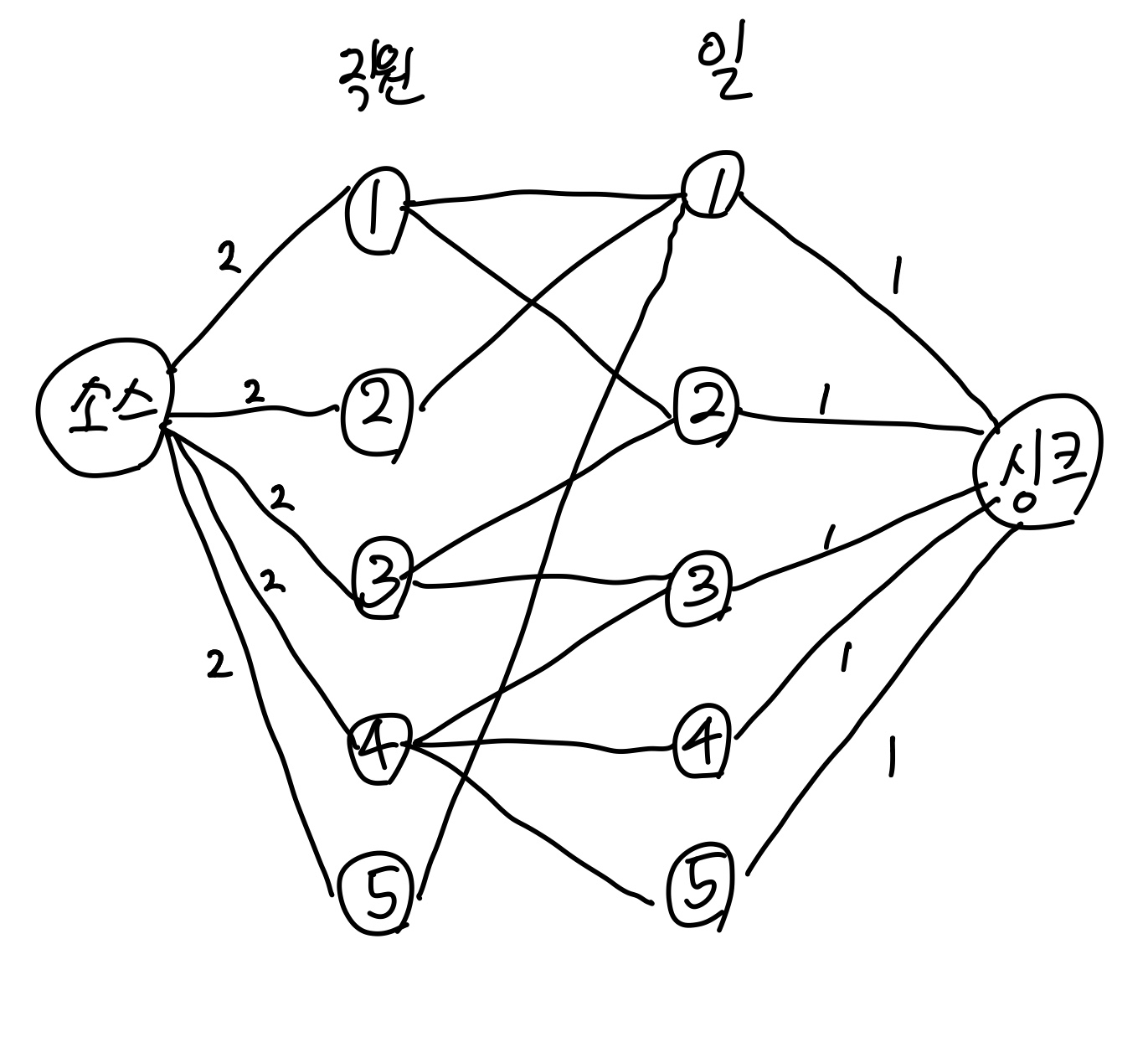
소스 -> 직원으로의 가중치가 2로 바뀌었다.
왜 why? 각 직원은 2개의 일을 할 수 있으니까.
3. 열혈강호3 (11377)
열혈강호 1, 2는 바로 풀었는데, 이건 고민이 조금 필요했다.
우선 열혈강호1과 굉장히 비슷하다. 하지만 이 문제에서는 N명 중에서 K명은 일을 2개까지 할 수 있다.
그러니까 뭐 대충 N+K개의 일을 할 수 있게 된다.
따라서 우선 소스->직원으로 흘려주는 양을 N+K로 하면 될 거라고 생각이 들었다.
그렇다면 어떤 직원에게 2를 흘려주고 어떤 직원에게 1을 흘려줘야 할까를 고민했는데, 답이 없었다.
왜냐하면 그리디?하게 알 수 있나 생각해 보았을 때, 알 수 없었다. 또, 완전 탐색은 시간 초과가 날 게 뻔했다.
그러다가 든 생각이 N개에 우선 용량 1을 주고 생각해보았다.
그러고 나니, 임시 노드 하나를 추가하여 용량을 1씩 더 주게 하였다. 참고로 임시 노드로 향하는 간선의 용량은 K로 두었다.
이렇게 되면 그냥 바로 열혈강호1과 같은 문제가 된다.
말로 하니 어려운 것 같은데, 그림으로 보자.
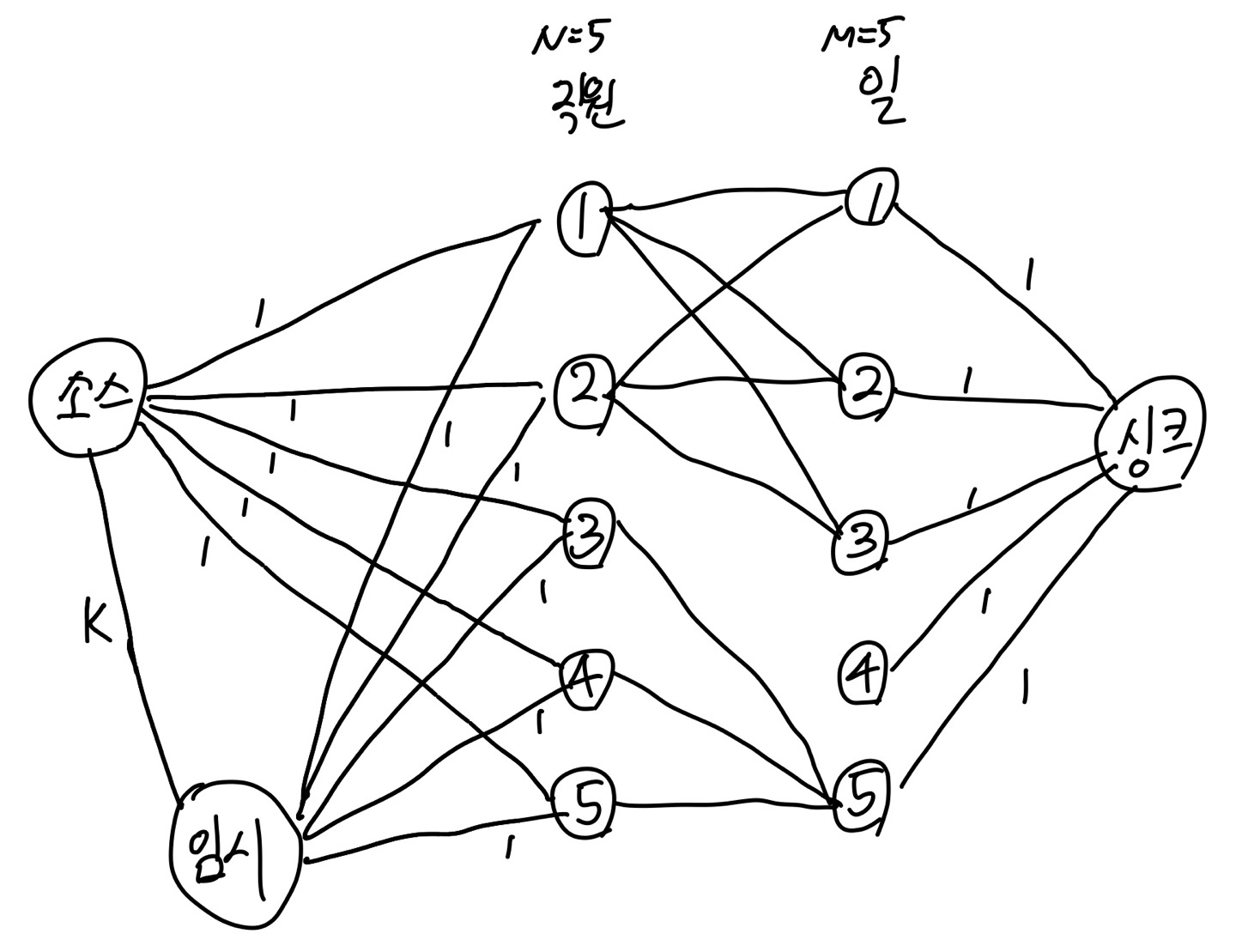
그니까 임시 노드를 추가하여 소스->임시 간선의 용량을 K로 하면 N+K를 흘려줄 수 있게 된다.
끝.
4. 열혈강호4 (11378)
문제가 되게 다른 거 같지만, 열혈강호3와 똑같다.
벌점을 받은 사람은 벌점만큼의 일을 더 할 수 있다. 그니까 총 벌점+1의 일을 할 수 있다.
이 문제에서는 벌점의 총 합은 정해져 있지만, 벌점을 자유롭게 배분할 수 있다.
그러니까 임시->직원으로 가는 간선의 용량을 무한대값으로 잡아준 뒤, 최대 유량을 구하면 알아서 잘 배분될 것이다.
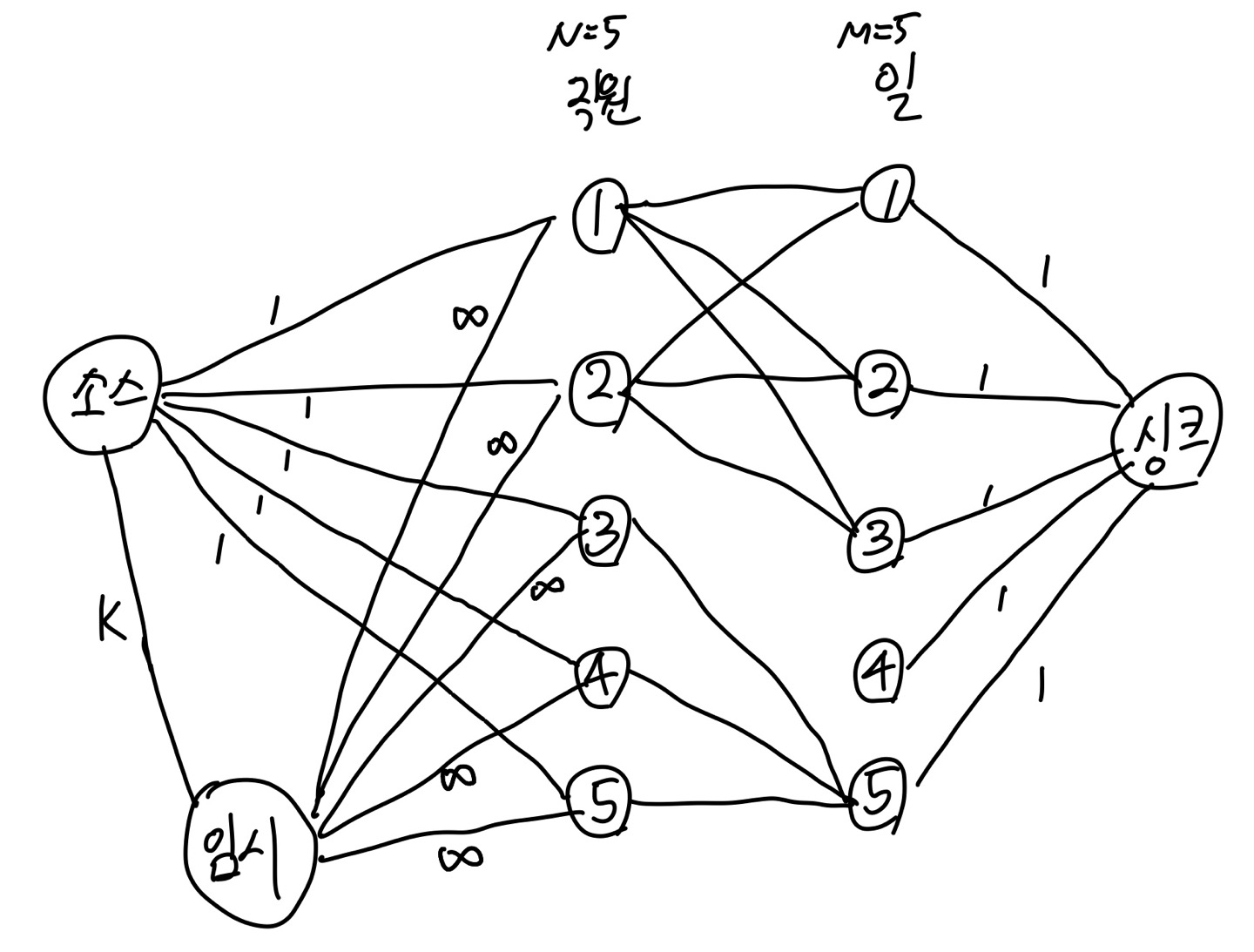
임시->직원 간선의 용량이 무한대인 것을 알 수 있다.
여담으로 이 문제가 열혈강호3보다 티어가 낮다. 나는 이 문제가 열혈강호3와 동등하거나 그 이상이라고 생각한다.
---아래는 풀면 업데이트 예정
5. 열혈강호5 (11408)
6. 열혈강호6 (11409)
---
열혈강호3, 4를 풀고 나서 생각난 건데, 그래프 문제에서 노드 하나를 추가하여 생각하는 방법을 예전에도 본 적이 있었다.
whcho0504가 SPC에 냈던 MST 문제가 있었다. boj.kr/23743
조건을 따져가면서 풀어도 되지만, 출구를 0번 노드로 두면 그냥 기본 MST문제와 똑같아졌던 기억이 있다.
전혀 다른 문제지만 신기해서 ㅎㅎ